线性回归是最简单同时也是最常用的一个统计模型。线性回归具有结果易于理解,计算量小等优点。如果一个简单的线性回归就能取得非常不错的预测效果,那么就没有必要采用复杂精深的模型了。
今天,我们一起来学习使用Python实现线性回归的几种方法:
- 通过公式编写矩阵运算程序;
- 通过使用机器学习库sklearn;
- 通过使用statmodels库。
这里,先由简至繁,先使用sklearn实现,再讲解矩阵推导实现。
1.使用scikit-learn进行线性回归
设置工作路径
#
import os
os.getcwd()
os.chdir('D:\my_python_workfile\Project\Writting')
加载扩展包
import pandas as pd
import numpy as np
import pylab as pl
import matplotlib.pyplot as plt
载入数据并可视化分析
这里,为了简单起见,使用sklearn中自带的数据集鸢尾花数据iris进行分析,探索『花瓣宽』和『花瓣长』之间的线性关系。
from sklearn.datasets import load_iris
# load data
iris = load_iris()
# Define a DataFrame
df = pd.DataFrame(iris.data, columns = iris.feature_names)
# take a look
df.head()
#len(df)
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
# correlation
df.corr()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| sepal length (cm) | 1.000000 | -0.109369 | 0.871754 | 0.817954 |
| sepal width (cm) | -0.109369 | 1.000000 | -0.420516 | -0.356544 |
| petal length (cm) | 0.871754 | -0.420516 | 1.000000 | 0.962757 |
| petal width (cm) | 0.817954 | -0.356544 | 0.962757 | 1.000000 |
# rename the column name
df.columns = ['sepal_length','sepal_width','petal_length','petal_width']
df.columns
Index([u'sepal_length', u'sepal_width', u'petal_length', u'petal_width'], dtype='object')
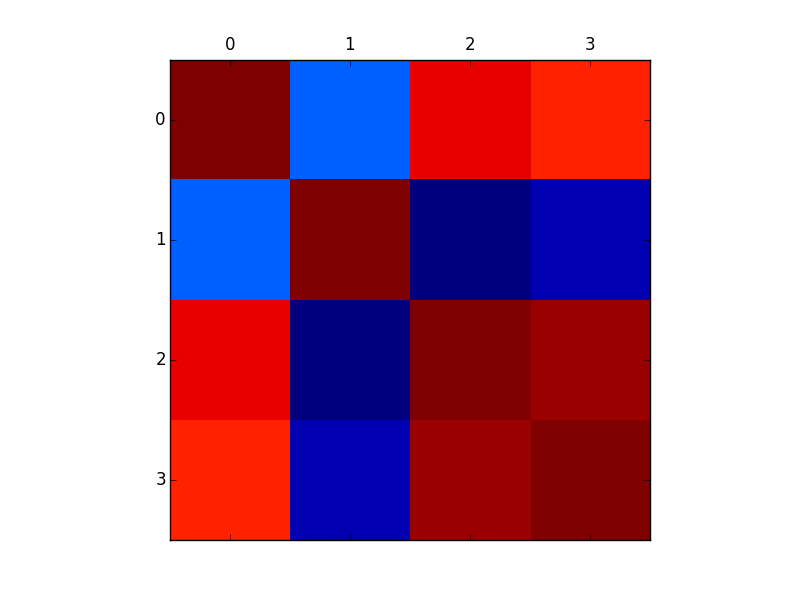
plt.matshow(df.corr())
由上面分析可知,花瓣长sepal length和花瓣宽septal width有着非常显著的相关性。
下面,通过线性回归进一步进行验证。
# save image
fig,ax = plt.subplots(nrows = 1, ncols = 1)
ax.matshow(df.corr())
fig.savefig('./image/iris_corr.png')
建立线性回归模型
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
X = df[['petal_length']]
y = df['petal_width']
lr.fit(X,y)
# print the result
lr.intercept_,lr.coef_
(-0.3665140452167297, array([ 0.41641913]))
# get y-hat
yhat = lr.predict(X = df[['petal_length']])
# MSE
mean_squared_error(df['petal_width'],yhat)
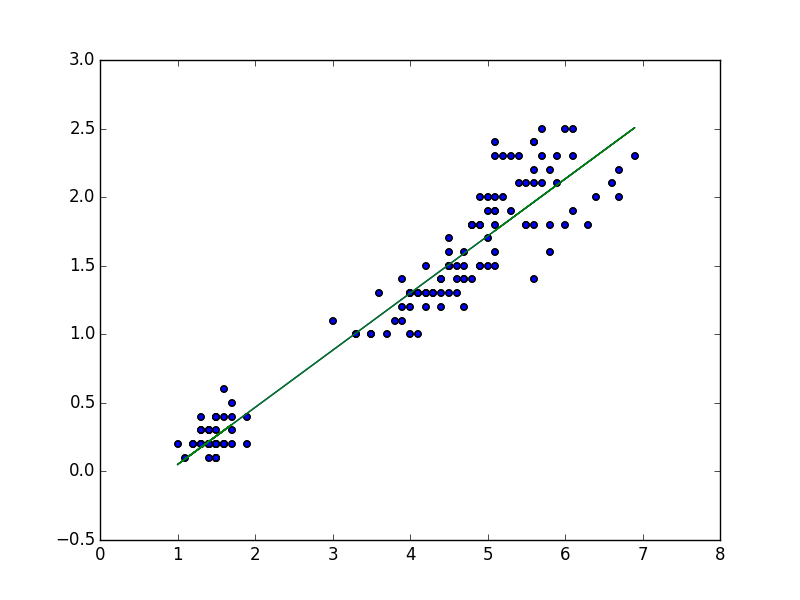
# lm plot
plt.scatter(df['petal_length'],df['petal_width'])
plt.plot(df['petal_length'],yhat)
#save image
plt.savefig('./image/iris_lm_fit.png')
2.使用statmodels库
#import statsmodels.api as sm
import statsmodels.formula.api as sm
linear_model = sm.OLS(y,X)
results = linear_model.fit()
results.summary()
| Dep. Variable: | petal_width | R-squared: | 0.967 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.967 |
| Method: | Least Squares | F-statistic: | 4372. |
| Date: | Mon, 14 Mar 2016 | Prob (F-statistic): | 2.55e-112 |
| Time: | 22:55:09 | Log-Likelihood: | -9.4520 |
| No. Observations: | 150 | AIC: | 20.90 |
| Df Residuals: | 149 | BIC: | 23.91 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [95.0% Conf. Int.] | |
|---|---|---|---|---|---|
| petal_length | 0.3364 | 0.005 | 66.124 | 0.000 | 0.326 0.346 |
| Omnibus: | 19.115 | Durbin-Watson: | 0.855 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 22.606 |
| Skew: | 0.940 | Prob(JB): | 1.23e-05 |
| Kurtosis: | 3.292 | Cond. No. | 1.00 |
3.使用公式推导
线性回归,即是使得如下目标函数最小化:
使用最小二乘法,不难得到的估计:
从而,我们可以根据此公式,编写求解的函数。
from numpy import *
#########################
# 定义相应的函数进行矩阵运算求解。
def standRegres(xArr, yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T * xMat
if linalg.det(xTx) == 0.0:
print "this matrix is singular, cannot do inverse!"
return NA
else :
ws = xTx.I * (xMat.T * yMat)
return ws
# test
x0 = np.ones((150,1))
x0 = pd.DataFrame(x0)
X0 = pd.concat([x0,X],axis = 1)
standRegres(X0,y)
matrix([[-0.36651405],
[ 0.41641913]])
结果一致。
参考文献
-
『机器学习实战』